Dispersion (Physik)

Dispersion im Prisma erzeugt ein Farbspektrum

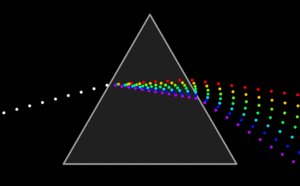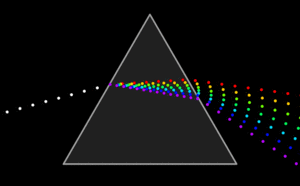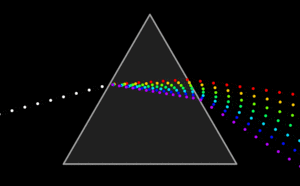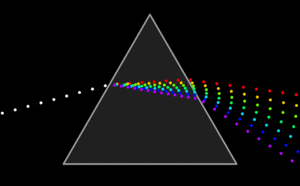
Unter Dispersion (von lateinisch dispergere, „ausbreiten, zerstreuen“) versteht man in der Physik die Abhängigkeit einer Größe von der Frequenz. In der Optik ist dies speziell die von der Frequenz des Lichts abhängende Ausbreitungsgeschwindigkeit des Lichts in Medien. Dies hat zur Folge, dass Sonnenlicht an den Flächen eines Prismas unterschiedlich stark gebrochen wird. Auf der anderen Seite des Prismas zeigt sich deshalb ein farbiges Spektrum.

Der Zusammenhang zwischen der Kreisfrequenz (oder den Energiequanten) einer harmonischen Welle und dem Wellenvektor wird Dispersionsrelation genannt. Insbesondere ist das in der Quantentheorie gerade der Energie-Impuls-Zusammenhang des Teilchens.

Normale und anomale Dispersion

Brechungsindex von Quarzglas in Abhängigkeit von der Wellenlänge (sichtbares Licht bis nahes Infrarot)

Einflüsse der Zugabe ausgewählter Glasbestandteile auf die optische Dispersion eines speziellen Basisglases.

Bei den meisten transparenten Stoffen steigt im sichtbaren Bereich der Brechungsindex mit der Frequenz an, Glas bricht blaues Licht stärker als rotes. Man spricht von normaler Dispersion. Eine positive Ableitung des Brechungsindex nach der Frequenz der Welle (${\text{d}}n/{\text{d}}\omega \,>\,0$) ist gleichbedeutend mit einer negativen Ableitung nach der Wellenlänge (${\text{d}}n/{\text{d}}\lambda \,<\,0$).

Fällt dagegen der Brechungsindex mit steigender Frequenz, so liegt eine anomale Dispersion vor. Entdeckt wurde sie bei einer alkoholischen Fuchsin-Lösung von Christian Christiansen im Jahr 1870. Der Effekt ist keine spezielle Eigenschaft dieses Farbstoffs, vielmehr tritt er immer in Wellenlängenbereichen nahe einer starken Absorption auf. Ganz allgemein verknüpft die Kramers-Kronig-Relation den Verlauf des Brechungsindex mit dem der Absorption.

Quantitative Beschreibung

Eine einfache Kennzahl für die Dispersion eines isotropen, transparenten Mediums ist die Abbe-Zahl. Die Sellmeier-Gleichung dagegen versucht, den empirisch ermittelten Verlauf des Brechungsindex $n$ über die Wellenlänge $\lambda$ genau wiederzugeben. Daneben existiert noch eine einfachere Beschreibung durch die Cauchy-Gleichung. Darüber hinaus gibt es noch zahlreiche weitere Dispersionsformeln, z. B.:

• Helmholtz-Ketteler-Drude-Dispersionsformel,
• Schottsche Dispersionsformeln,
• Geffckensche Dispersionsformel,
• Buchdahlsche Dispersionsformel,
• Kettlersche Dispersionsformel,
• Kramers-Heisenbergsche Dispersionsformel,
• Breit-Wignersche Dispersionsformel,
• Hartmannsche Dispersionsformel,
• Herzbergsche Dispersionsformel (für den visuellen Bereich ) oder
• als Polynomformel: $n^{2}(\lambda )=\sum _{i=1}^{6}A_{i}\lambda ^{4-2i}$

Auswirkungen

Die Dispersion der Phasengeschwindigkeit bestimmt die Dispersion der Gruppengeschwindigkeit.

Dispersion der Phasengeschwindigkeit

• Ein Prisma zerlegt Licht in sein Farbspektrum.
• Abbildungen mittels Linsen zeigen unerwünschte Farbränder, die durch Kombination von Linsen aus optischen Gläsern unterschiedlicher Dispersion korrigiert werden können (siehe Achromat und Apochromat).
• Auch magnetische Linsen etwa eines Elektronenmikroskops zeigen Dispersion in Abhängigkeit von der Geschwindigkeit der Elektronen. Gegenmaßnahmen sind eine schmale Energieverteilung der Elektronen, aus Feld- statt Glühemission, eine hohe Beschleunigungsspannung und eine kleine Apertur.

Dispersion der Gruppengeschwindigkeit

• Lichtimpulse in Glasfasern, welche beispielsweise in der optischen Datenübertragung eingesetzt werden, erfahren auf Grund der Dispersion der Gruppengeschwindigkeit eine Verbreiterung während der Übertragung. Je geringer die Dauer eines Lichtimpulses ist, desto breiter ist sein Frequenzspektrum und desto ausgeprägter ist die Änderung der Impulsform, besonders auf langen Übertragungsstrecken (siehe Dispersion in Lichtwellenleitern).
• Elektrische Kabel weisen je nach Frequenz aufgrund ihrer Isolierstoffe unterschiedliche Ausbreitungsgeschwindigkeiten auf, was sich z. B. bei der Zeitbereichsreflektometrie an verbreiterten reflektierten Impulsen zeigt. Der Effekt führt zu Laufzeitverzerrungen bei breitbandigen Signalen (zum Beispiel in Form von flacheren Impulsflanken) und kann durch geeignete Isolierstoffe vermieden werden.

Beispiele

Die Dispersion von Wasserwellen wird in Dispersion (Wasserwellen) beschrieben; die Dispersionsrelation von Phononen im dortigen Abschnitt Dispersion. In Lichtwellenleitern gibt es außerdem Polarisationsmodendispersion.