| Jewiki unterstützen. Jewiki, die größte Online-Enzyklopädie zum Judentum.
Helfen Sie Jewiki mit einer kleinen oder auch größeren Spende. Einmalig oder regelmäßig, damit die Zukunft von Jewiki gesichert bleibt ... Vielen Dank für Ihr Engagement! (→ Spendenkonten) |
How to read Jewiki in your desired language · Comment lire Jewiki dans votre langue préférée · Cómo leer Jewiki en su idioma preferido · בשפה הרצויה Jewiki כיצד לקרוא · Как читать Jewiki на предпочитаемом вами языке · كيف تقرأ Jewiki باللغة التي تريدها · Como ler o Jewiki na sua língua preferida |
Raute
Ein ebenes Viereck, bei dem alle vier Seiten gleich lang sind, heißt Raute (Plural: Rauten) oder Rhombus (Plural: Rhomben). Dabei sind gegenüberliegende Seiten parallel und gegenüberliegende Winkel gleich groß.
Darstellungen und Bezeichnungen
Die Symboldarstellungen befinden sich im Unicode-Block Geometrische Formen. Das Zeichen U+25C6 ◆ heißt „schwarze Raute“, U+25C7 ◇ „weiße Raute“, U+25CA ◊ „Rhombus“.
Neben Raute und Rhombus wird manchmal auch der Ausdruck Karo verwendet. Heraldische Stilelemente heißen auch Wecke und Spindel.
Das Doppelkreuz # wird fälschlicherweise oft in Verbindung mit Telefon- und Computertastaturen als Raute bezeichnet.
Mitunter werden auch Parallelogramme als Rauten bezeichnet. Die Raute ist jedoch nur eine Spezialform des Parallelogramms. Ein Spezialfall der Raute wiederum ist das Quadrat, das, auf der Spitze stehend, manchmal ebenfalls verallgemeinernd als Raute bezeichnet wird (heraldisch Kantenwürfel). Das hat seine Ursache darin, dass mit dem Begriff Quadrat manchmal nur seine kantenparallele Darstellung im Bezugssystem assoziiert wird. Im Extremfall der Spitzendarstellung wird es dann als ein anderes Objekt angesehen und bekommt somit auch einen anderen Namen.
Geometrie
Eine Raute oder ein Rhombus ist ein ebenes Viereck mit vier gleich langen Seiten (gleichseitiges Viereck).
- Folgerungen
- Es ist konvex.
- Gegenüberliegende Seiten sind parallel.
- Die beiden Diagonalen sind Symmetrieachsen.
- Die Diagonalen stehen senkrecht aufeinander und halbieren einander.
- Gegenüberliegende Winkel sind gleich groß; benachbarte Winkel ergänzen einander auf 180°.
- Jeder Innenwinkel wird durch eine Diagonale halbiert.
- Jede Raute besitzt einen Inkreis, aber nur die rechtwinkelige (also das Quadrat) einen Umkreis.
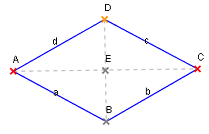
Die Raute ist ein Drachenviereck mit paarweise parallelen Seiten. Eine Raute, für die man einen rechten Winkel fordert, ist schon ein Quadrat. Um eine Raute zu konstruieren, sind zwei Bestimmungsstücke (wie zum Beispiel die Seitenlänge a und einer der beiden Winkel) notwendig.
| Formeln zur Raute (zum Rhombus) | ||
|---|---|---|
| Flächeninhalt | Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A \, = \frac{1}{2} \cdot \overline{AC} \cdot \overline{BD} }
Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A \, = \, a \cdot h_a = b \cdot h_b }
| |
| Umfang | Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle u \, = \, 4 \cdot a} | |
| Diagonalenlänge | Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle e \, = \, 2 \cdot a \cdot \cos\frac{\alpha}{2} = 2 \cdot a \cdot \sin\frac{\beta}{2}} | |
| Diagonalenlänge | Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f \, = \, 2 \cdot a \cdot \sin\frac{\alpha}{2} = 2 \cdot a \cdot \cos\frac{\beta}{2}} | |
| Inkreisradius | Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \rho \, = \, \frac{1}{2} \cdot a \cdot \sin\alpha} | |
| Länge einer Seite | Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a\, = \, \sqrt{\left(\frac{e}{2}\right )^2+\left(\frac{f}{2}\right )^2 }} | |
| Größe des Innenwinkels bei A | Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha\,} | |
| Größe des Innenwinkels bei B | Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta\,} | |
| Diagonalenlängen | Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle e = \overline{AC}; \quad f = \overline{BD}} | |
Vorkommen und Anwendung
Zum Stern schließen sich nur diejenigen Rhomben, die die Bedingung erfüllen, dass der Zentriwinkel, also der Winkel in der Spitze, in der man sie aneinanderlegt, gleich Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{360^\circ}{n}} für eine natürliche Zahl Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n} ist. Sie bilden dann einen n-zackigen Stern. Das gilt nicht für den dreidimensionalen Fall, hierbei lassen sich auch anderswinklige Rhomben in ihrer Spitze aneinanderfügen, und ergeben dann pyramidenförmige Spitzen.
- Praktische Anwendungen:
- Rautensterne wirken neutral, Sterne aus Trapezen spitz, also dynamisch, wenn die lange Halbdiagonale außen liegt, andernfalls stumpf. Das wird im Dekorationswesen bewusst verwendet.
- Das Rhombendach ist aus vier rautenförmigen Dachflächen zusammengesetzt. Es erlaubt zu quadratischen Grundrissen um 45 Grad versetzte Dachschrägen (die das Wasser nicht über die Portale ableiten).
Dachlösung in Rauten (Marienkirche (Dortmund))
Durch seine Definition eignet sich jeder Rhombus für eine flächendeckende Kachelung, aber nur in zwei Hauptrichtungen (platonische Parkettierung). Hier bildet die Rautenparkettierung (mit ihrer Sonderform, dem Quadratgitter, also einem orthogonalen Raster) eine der 17 möglichen Symmetriegruppen der Parkettierungen.[1]
- eine Besonderheit ist die aperiodische (quasikristalline) Penrose-Parkettierung zweier Rauten mit 36°/144° und 72°/108°.
- Technische Anwendungen:
- Dachflächen werden in Rautendeckung geschlossen. Diese hat gute Wasserleiteigenschaften, da das Wasser an der unteren Spitze abtropft, und braucht nur eine Nagelung an der oberen Spitze. Sie eignet sich für Flachformplatten wie Eternit oder Blechschindeln und wurde auch bei Holzschindelzierat angewandt.
- Bei der Rhombus- oder Rauten-Schalung handelt es sich im mathematischen Sinne meist nicht um rautenförmige Holzprofile, sondern um Parallelogramme (Querschnitt der liegend montierten Schallatten, die dann ebenfalls eine definierte Tropfkante haben).
Flächenfüllende, schiefwinklig-platonische Kachelung als Dekorationsmuster (Staatsflagge Bayerns (Rautenflagge), heraldische Fachsprache: gerautet)
Rhombenparketierung mit 3D-Effekt (Kolorierungvariante des Dreieckgitters)
Ein Rhomboeder ist ein Polyeder, dessen Körper ausschließlich von Rauten begrenzt ist.
Weblinks
Commons: Raute – Sammlung von Bildern
- Wiktionary: Raute – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen
- Weiterführende Informationen, Berechnungsbeispiele und Abbildungen
- Beschreibung einer Raute inklusive Konstruktion und Herleitung
Einzelnachweise
- ↑ Bewiesen von Jewgraf S. Fedorow 1891, nach Ian Stewart: Fünfeckige Kacheln. In: Spektrum der Wissenschaft, Januar 2000, S. 106–108 (Abb. S. 108)
| Dieser Artikel basiert ursprünglich auf dem Artikel Raute aus der freien Enzyklopädie Wikipedia und steht unter der Doppellizenz GNU-Lizenz für freie Dokumentation und Creative Commons CC-BY-SA 3.0 Unported. In der Wikipedia ist eine Liste der ursprünglichen Wikipedia-Autoren verfügbar. |