Riemannsches Integral

Das Riemannsche Integral (auch Riemann-Integral) ist eine nach dem deutschen Mathematiker Bernhard Riemann benannte Methode zur Präzisierung der anschaulichen Vorstellung des Flächeninhaltes zwischen der Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} -Achse und dem Graphen einer Funktion. Der riemannsche Integralbegriff gehört neben dem allgemeineren lebesgueschen zu den beiden klassischen der Analysis. In vielen Anwendungen werden nur Integrale von stetigen oder stückweise stetigen Funktionen benötigt. Dann genügt der etwas einfachere, aber weniger allgemeine Begriff des Integrals von Regelfunktionen.

Das dem Riemannschen Integral zu Grunde liegende Konzept besteht darin, den gesuchten Flächeninhalt mit Hilfe des leicht zu berechnenden Flächeninhalts von Rechtecken anzunähern. Man geht dabei so vor, dass man in jedem Schritt zwei Familien von Rechtecken so wählt, dass der Graph der Funktion „zwischen“ ihnen liegt. Indem man sukzessive die Anzahl der Rechtecke erhöht, erhält man mit der Zeit eine immer genauere Annäherung des Funktionsgraphen durch die zu den Rechtecken gehörenden Treppenfunktionen. Entsprechend lässt sich der Flächeninhalt zwischen dem Graphen und der Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} -Achse durch die Flächeninhalte der Rechtecke approximieren.

Definitionen

Es gibt im Wesentlichen zwei gängige Verfahren zur Definition des Riemann-Integrals:

• das Jean Gaston Darboux zugeschriebene Verfahren mittels Ober- und Untersummen und
• Riemanns ursprüngliches Verfahren mittels Riemann-Summen.

Die beiden Definitionen sind äquivalent: Jede Funktion ist genau dann im darbouxschen Sinne integrierbar, wenn sie im riemannschen Sinne integrierbar ist; in diesem Fall stimmen die Werte der beiden Integrale überein. In typischen Analysis-Einführungen, vor allem in der Schule, wird heute weitgehend die Darbouxsche Formulierung zur Definition benutzt. Riemannsche Summen treten oft als weiteres Hilfsmittel hinzu, etwa zum Beweis des Hauptsatzes der Integral- und Differenzialrechnung.

Ober- und Untersummen

Dieser Zugang wird meist Jean Gaston Darboux zugeschrieben.

Untersumme (grün) und Obersumme (grün plus lavendel) für eine Zerlegung in vier Teilintervalle

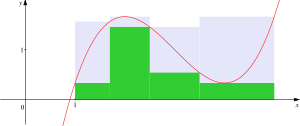
Das Integrationsintervall wird hierbei in kleinere Stücke zerlegt, der gesuchte Flächeninhalt zerfällt dabei in senkrechte Streifen. Für jeden dieser Streifen wird nun einerseits das größte Rechteck betrachtet, das von der Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} -Achse ausgehend den Graphen nicht schneidet (im Bild grün), und andererseits das kleinste Rechteck, das von der Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} -Achse ausgehend den Graphen ganz umfasst (im Bild jeweils das grüne Rechteck zusammen mit der grauen Ergänzung darüber). Die Summe der Flächeninhalte der großen Rechtecke wird als Obersumme, die der kleinen als Untersumme bezeichnet. Kann man durch geeignete, ausreichend feine Unterteilung des Integrationsintervalles den Unterschied zwischen Ober- und Untersumme beliebig klein machen, so gibt es nur eine Zahl, die kleiner oder gleich jeder Obersumme und größer oder gleich jeder Untersumme ist, und diese Zahl ist der gesuchte Flächeninhalt, das Riemannsche Integral.

Für die mathematische Präzisierung seien im Folgenden Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle [a,b]} ein Intervall und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f\colon[a,b]\to\R} eine beschränkte Funktion.

Unter einer Zerlegung Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Z} von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle [a,b]} in Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n} Teile versteht man eine endliche Folge Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_0,x_1,\dotsc,x_n} mit Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a=x_0<x_1<\dotsb<x_n=b} . Dann werden die zu dieser Zerlegung gehörende Ober- und Untersumme definiert als

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle O(Z):=\sum_{k=1}^n \Big( (x_k-x_{k-1})\cdot\sup_{x_{k-1}<x<x_k}f(x) \Big)}

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U(Z):=\sum_{k=1}^n \Big( (x_k-x_{k-1})\cdot\inf_{x_{k-1}<x<x_k}f(x) \Big)} .

Die Funktion wird dabei durch die Treppenfunktion ersetzt, die auf jedem Teilintervall konstant gleich dem Supremum beziehungsweise Infimum der Funktion auf diesem Intervall ist.

Bei einer feineren Unterteilung wird die Obersumme kleiner und die Untersumme größer

Bei einer Verfeinerung der Zerlegung wird die Obersumme kleiner, die Untersumme größer (oder sie bleiben gleich). Einer „unendlich feinen“ Zerlegung entsprechen also Infimum der Obersummen sowie Supremum der Untersummen; diese werden als oberes beziehungsweise unteres darbouxsches Integral von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f} bezeichnet:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \overline{\int_a^b}f(x)\,\mathrm dx:=\inf_ZO(Z) := \inf \{ O(Z) : Z \mbox{ ist Zerlegung von } [a,b] \}}

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \underline{\int_a^b}f(x)\,\mathrm dx:=\sup_ZU(Z):= \sup \{ U(Z) : Z \mbox{ ist Zerlegung von } [a,b] \}} .

Es werden also jeweils alle möglichen Zerlegungen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Z} des Intervalls in eine beliebige endliche Anzahl von Teilintervallen betrachtet.

Beispiel der Zerlegung eines Intervalls [a,b] in n=8 Teile (Obersumme lila und Untersumme orange)

Es gilt stets

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \underline{\int_a^b}f(x)\,\mathrm dx\leq\overline{\int_a^b}f(x)\,\mathrm dx.}

Gilt Gleichheit, so heißt Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f} Riemann-integrierbar (oder Darboux-integrierbar), und der gemeinsame Wert

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \int_a^bf(x)\,\mathrm dx:=\underline{\int_a^b}f(x)\,\mathrm dx=\overline{\int_a^b}f(x)\,\mathrm dx}

heißt das Riemannsche Integral (oder Darboux-Integral) von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f} über dem Intervall Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle [a,b]} .

Riemann-Summen

Der obige Zugang zum Riemann-Integral über Ober- und Untersummen stammt, wie dort beschrieben, nicht von Riemann selbst, sondern von Jean Gaston Darboux. Riemann untersuchte zu einer Zerlegung Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Z = \{ a = x_0, x_1, \dotsc,x_n = b\}} des Intervalls Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle [a,b]} und zu Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Z} gehörigen Zwischenstellen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t_i \in [x_{i-1}, x_i] (i=1,\dotsc,n)} Summen der Form

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S(f, Z, t_1,\dotsc,t_n) = \sum_{i=1}^n f(t_i) (x_i - x_{i-1}),}

Geometrische Veranschaulichung der riemannschen Zwischensummen (orange Rechtecke). Es gilt für die gezeigte Zerlegung Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Z\colon \mu(Z) = x_7 - x_6}

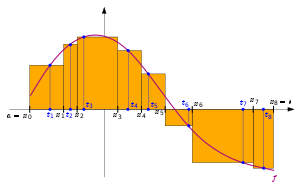
auch als Riemann-Summen oder Riemannsche Zwischensummen bezüglich der Zerlegung Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Z} und den Zwischenstellen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t_1,\dotsc,t_n} bezeichnet. Riemann nannte eine Funktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f} über dem Intervall Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle [a,b]} integrierbar, wenn sich die Riemann-Summen bezüglich beliebiger Zerlegungen unabhängig von den gewählten Zwischenstellen einer festen Zahl Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A} beliebig nähern, sofern man die Zerlegungen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Z} nur hinreichend fein wählt. Die Feinheit einer Zerlegung Z wird dabei über die Länge des größten Teilintervalls Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle [x_{i-1}, x_i]} , das durch Z gegeben ist, gemessen, also durch die Zahl:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu(Z) = \max \{ x_{i} - x_{i-1} : i=1,\dotsc,n\}.}

Die Zahl Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A} ist dann das Riemann-Integral von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f} über Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle [a,b]} . Ersetzt man die Veranschaulichungen „hinreichend fein“ und „beliebig nähern“ durch eine präzise Formulierung, so lässt sich diese Idee wie folgt formalisieren.

Eine Funktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f\colon [a,b] \rightarrow \mathbb R} heißt über dem Intervall Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle [a,b]} Riemann-integrierbar, wenn es zu einer festen Zahl Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A} und zu jedem Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varepsilon > 0} ein Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \delta > 0} gibt, so dass für jede Zerlegung Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Z} mit Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu(Z) < \delta} und für beliebige zu Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Z} gehörige Zwischenstellen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t_1,\dotsc,t_n}

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle |S(f, Z, t_1,\dotsc,t_n) - A | < \varepsilon}

gilt. Die Zahl Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A} heißt dann das Riemann-Integral von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f} über Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle [a,b]} und man schreibt dafür

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A = \int_a^b f} oder Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \displaystyle A = \int_a^b f(x) \; \mathrm dx} .

Riemann-Integrierbarkeit

Lebesgue-Kriterium

Eine Funktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f} ist nach dem Lebesgue'schen Kriterium für Riemann-Integrierbarkeit genau dann auf dem kompakten Intervall Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle [a,b]} Riemann-integrierbar, falls sie auf dem Intervall beschränkt und fast überall stetig ist. Falls die Funktion Riemann-integrierbar ist, so ist sie auch Lebesgue-integrierbar und beide Integrale sind identisch.

Insbesondere ist über einem kompakten Intervall jede Regelfunktion, jede monoton wachsende oder monoton abnehmende Funktion und jede stetige Funktion Riemann-integrierbar.

Beispiele

Die Funktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f \colon [0,1] \to [0,1]} mit

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f(x) = \begin{cases} 1 & ~\text{falls}~ x=0 \\ \frac 1 q & ~\text{falls}~ x=\frac r q ~\text{mit}~ r,q \in \N ~\text{teilerfremd} \\ 0 & ~\text{falls}~ x \in \R \setminus \Q \end{cases}}

ist stetig in allen irrationalen Zahlen und unstetig in allen rationalen Zahlen. Die Menge der Unstetigkeitsstellen liegt zwar dicht im Definitionsbereich, da diese Menge aber abzählbar ist, ist sie eine Nullmenge. Die Funktion ist damit Riemann-integrierbar.

Die Dirichlet-Funktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g \colon [0,1] \to [0,1]} mit

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g(x) = \begin{cases} 1 & ~\text{falls}~ x \in \Q \\ 0 & ~\text{falls}~ x \in \R \setminus \Q \end{cases}}

ist nirgendwo stetig, sie ist also nicht Riemann-integrierbar. Sie ist aber Lebesgue-integrierbar, da sie fast überall Null ist.

Die Funktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h \colon [-1,1] \to [0,1]} mit

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h(x) = \begin{cases} 1 & ~\text{falls}~ x \in \{ \frac 1 n \mid n \in \N \} \\ 0 & ~\text{sonst}~ \end{cases}}

hat abzählbar viele Unstetigkeitsstellen, ist also Riemann-integrierbar. Bei Null existieren die rechts- und linksseitigen Grenzwerte nicht. Die Funktion hat dort daher eine Unstetigkeitsstelle der zweiten Art. Die Funktion ist somit keine Regelfunktion, das heißt, sie lässt sich nicht gleichmäßig durch Treppenfunktionen approximieren. Das Riemann-Integral erweitert also das Integral, das über den Grenzwert von Treppenfunktionen von Regelfunktionen definiert ist.

Uneigentliche Riemann-Integrale

Als uneigentliche Riemann-Integrale bezeichnet man:

• Integrale mit den Intervallgrenzen Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle -\infty} oder Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \infty} ; dabei ist

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \int_{a}^\infty f(x) \,\mathrm{d}x = \lim_{\beta \to \infty}\int_a^{\beta}f(x) \,\mathrm{d}x} ,

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \int_{-\infty}^{b}f(x)\,\mathrm{d}x = \lim_{\alpha \to -\infty}\int_\alpha^b f(x) \,\mathrm{d}x} und

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \int_{-\infty}^{\infty} f(x) \,\mathrm{d}x = \int_{-\infty}^{a}f(x)\,\mathrm{d}x+\int_{a}^\infty f(x) \,\mathrm{d}x} mit beliebigem Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a\in\mathbb{R}.}

• Integrale mit unbeschränkten Funktionen in einer der Intervallgrenzen; dabei ist

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \int_a^b f(x) \,\mathrm{d}x = \lim_{\varepsilon \searrow 0} \int_{a+\varepsilon}^b f(x) \,\mathrm{d}x} bzw. Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \displaystyle\int_a^b f(x) \,\mathrm{d}x = \lim_{\varepsilon \searrow 0} \int_a^{b-\varepsilon} f(x) \,\mathrm{d}x.}

Mehrdimensionales Riemannsches Integral

Das mehrdimensionale Riemann-Integral basiert auf dem Jordan-Maß. Sei Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu_n} das n-dimensionale Jordan-Maß und sei Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E \subset \R^n} eine jordan-messbare Teilmenge. Außerdem sei Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \tau = (E_i)_{i=0}^k} eine endliche Folge von Teilmengen von Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E} mit Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \textstyle\bigcup\nolimits_{i=0}^k E_i = E} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu_n(E_i \cap E_j) = 0} für Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle i \neq j} und sei weiter Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \textstyle \operatorname{diam}(A) = \sup_{a,b \in \overline{A}}^{\,}(\|a-b\|)} die Funktion, welche die maximale Distanz in einer Menge Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A} zurückgibt. Setze nun

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \delta_\tau = \max_{i=0, \dotsc, k}\left(\operatorname{diam}(E_i)\right) = \max_{i=0, \dotsc, k}\left(\sup_{a,b \in \overline{E_i}}^{\,}(\|a-b\|)\right)} .

Sei Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f \colon E \to \R} eine Funktion, dann heißt die Summe

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \rho_\tau(f,\xi^{(0)},\dotsc , \xi^{(k)}) = \sum_{i=0}^{k(\delta_\tau)} f(\xi^{(i)})\mu_n(E_i)}

Riemannsche Zerlegung der Funktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f} .

Existiert der Grenzwert

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lim_{\delta_\tau \to 0}\rho_\tau(f,\xi^{(0)},\dotsc, \xi^{(k)}) = \lim_{\delta_\tau \to 0} \sum_{i=0}^{k(\delta_\tau)} f(\xi^{(i)})\mu_n(E_i)} ,

so ist die Funktion Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f} riemann-integrierbar und man setzt

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \int_E f(x) \mathrm{d} x = \lim_{\delta_\tau \to 0} \sum_{i=0}^{k(\delta_\tau)} f(\xi^{(i)})\mu_n(E_i)} .

Dieser Integralbegriff hat die gewöhnlichen Eigenschaften eines Integrals, die Integralfunktion ist linear und es gilt der Satz von Fubini.

Quellen

• Bernhard Riemann: Ueber die Darstellbarkeit einer Function durch eine trigonometrische Reihe. 1854 (Habilitationsschrift mit Begründung des nach ihm benannten Integralbegriffs).
• Harro Heuser: Lehrbuch der Analysis 1. 9. Auflage. Teubner, Stuttgart 1991, ISBN 3-519-22231-0 (insbesondere Abschnitt 82).
• Douglas S. Kurtz, Charles W. Swartz: Theories of Integration. World Scientific, New Jersey 2004, ISBN 981-256-611-2.

Weblinks

• Visualisierung des Riemannschen Integrals bei GeoGebra
• Visualisierung des Riemannschen Integrals bei Visual Calculus
• Visualisierung des Riemannschen Integrals auf mathe-online
• Mehrdimensionale Integrale bei Springer