Äquivokation

Äquivokation (von lateinisch aequus ,gleich‘ und vocare ,rufen‘) ist die Information, die bei der Übertragung über einen Kanal zwischen einer Informationsquelle (Sender) und einer Informationssenke (Empfänger) verloren geht. Der Terminus ist in diesem Zusammenhang als Informationsgehalt zu verstehen und geht auf die Informationstheorie von Claude Shannon zurück, welcher die Grundlagen für diese in den 1940er Jahren legte.
Der abstrakte Begriff eines „Informationskanals“ kann sich in praktischen Realisierungen über den Ort (z. B. eine Nachrichtenverbindung zwischen zwei Punkten; → PTP) oder über die Zeit (z. B. in Form eines Datenspeichers) erstrecken.

Definition

Modell eines Kanals mit Quelle H(X) und Senke H(Y) und der Äquivokation H(X|Y)

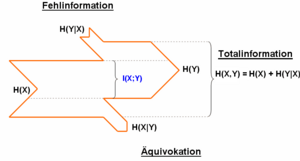
Die mathematische Definition des Informationsgehalts ist eng an die Entropiefunktion $H(A)$ gekoppelt, wobei die Zufallsvariable $A$ die Menge aller möglichen Symbole im Übertragungskanal beschreibt. Eine Informationsquelle sendet nun, wie in rechter Abbildung dargestellt, $H(X)$ über einen Kanal zur Informationssenke welche $H(Y)$ empfängt. $Y$ kann zu $X$ zufolge einer am Kanal eingebrachten Fehlinformation $H(Y|X)$ bzw. zufolge der am Kanal auftretenden Äquivokation $H(X|Y)$ unterschiedlich sein. Die Schreibweise $H(A|B)$ steht für die bedingte Entropie mit den beiden Zufallsvariablen $A,B$.

Als bedingte Entropiefunktion $H(X|Y)$ lässt sich die Äquivokation, mit $I(X;Y)$ der Transinformation zwischen Quelle und Senke, ausdrücken als:

$H(X|Y)=H(X)-I(X;Y)$

Als eine Wahrscheinlichkeitsfunktion $P(.)$ lässt sich die Äquivokation mit dem Logarithmus zur Basis 2 ausdrücken als:

$-\sum _{i}\sum _{j}P(x_{i},y_{i})\log _{2}P(x_{i}|y_{j})$

Quellen

• Jürgen Lindner: Informationsübertragung. Springer Verlag, Berlin Heidelberg 2005, ISBN 3-540-21400-3, S. 313.