| Jewiki unterstützen. Jewiki, die größte Online-Enzyklopädie zum Judentum.
Helfen Sie Jewiki mit einer kleinen oder auch größeren Spende. Einmalig oder regelmäßig, damit die Zukunft von Jewiki gesichert bleibt ... Vielen Dank für Ihr Engagement! (→ Spendenkonten) |
How to read Jewiki in your desired language · Comment lire Jewiki dans votre langue préférée · Cómo leer Jewiki en su idioma preferido · בשפה הרצויה Jewiki כיצד לקרוא · Как читать Jewiki на предпочитаемом вами языке · كيف تقرأ Jewiki باللغة التي تريدها · Como ler o Jewiki na sua língua preferida |
Claudius Ptolemäus

Claudius Ptolemäus (griechisch Κλαύδιος Πτολεμαῖος Klaúdios Ptolemaíos, lateinisch Claudius Ptolomaeus; geb. um 100, möglicherweise in Ptolemais Hermeiou, Ägypten; gest. vor 180, vermutlich in Alexandria)[1] war ein griechischer Mathematiker, Geograph, Astronom, Astrologe, Musiktheoretiker und Philosoph. Ptolemäus wirkte als Bibliothekar an der berühmten antiken Bibliothek in Alexandria. Insbesondere seine drei Werke zur Astronomie, Geografie und Astrologie galten in Europa bis in die frühe Neuzeit als wichtige umfangreiche Datensammlungen und wissenschaftliche Standardwerke.
So schrieb Ptolemäus die Mathematike Syntaxis („mathematische Zusammenstellung“), später Megiste Syntaxis („größte Zusammenstellung“), heute Almagest (abgeleitet vom Arabischen al-maǧisṭī) genannte Abhandlung zur Mathematik und Astronomie in 13 Büchern. Sie war bis zum Ende des Mittelalters ein Standardwerk der Astronomie und enthielt neben einem ausführlichen Sternenkatalog eine Verfeinerung des von Hipparchos von Nicäa vorgeschlagenen geozentrischen Weltbildes, das später nach ihm Ptolemäisches Weltbild genannt wurde.
Damit verwarf er wie der größte Teil seiner Zeitgenossen das von Aristarchos von Samos und Seleukos von Seleukia vertretene heliozentrische Weltbild, das erst 1300 Jahre später durch Nikolaus Kopernikus, Johannes Kepler und Galileo Galilei in Europa durchgesetzt werden sollte.
Astronomie
Ptolemäisches Weltbild
Nach Ptolemäus befindet sich die Erde fest im Mittelpunkt des Weltalls. Alle anderen Himmelskörper (Mond, Sonne, die 5 Planeten und der Sternhimmel) bewegen sich in kristallenen Sphären auf als vollkommen angesehenen Kreisbahnen (Deferent) um diesen Mittelpunkt. Um astronomische Beobachtungen mit diesem System in Einklang zu bringen, war es allerdings notwendig, alle Himmelskörper auf ihren Bahnen weitere Kreise (Epizykel) um diese Deferenten ziehen zu lassen – siehe Epizykeltheorie – und teilweise noch weitere Bewegungen um die primären Epizykel. Durch den Einsatz solcher (gegeneinander leicht geneigter) Bahnen konnte Ptolemäus sein Modell mit den damals noch freiäugigen Beobachtungen in Einklang bringen.
In der Sprache heutiger Mathematik könnte man Ptolemäus’ Berechnungsart als empirischen Vorläufer der Fourieranalyse bezeichnen, mit der die sekundären Perioden der Planetenbahnen (u.a. die Mittelpunktsgleichung) empirisch bestimmt wurden.
Das ptolemäische Weltbild war in der Genauigkeit seiner Bahnvorhersage dem heliozentrischen Weltbild des Nikolaus Kopernikus (16. Jhdt) überlegen. Das ptolemäische System wurde um 1600 durch das ebenfalls noch geozentrische tychonische Weltsystem (benannt nach Tycho Brahe) abgelöst. Erst Keplers Entdeckung, dass die Planeten auf Ellipsen um die Sonne laufen, führte dann zu einem damals ausreichend genauen und unter Astronomen allgemein akzeptierten Modell des kopernikanischen Weltbildes. Ptolemäus’ Berechnungsmethoden waren äußerst präzise (lange Zeit auch präziser als die Keplerschen) und in ihrer Grundidee als Berechnungsmethode auch richtig, nicht allerdings in ihrer philosophischen Deutung, dass sich alles um die Erde als Mittelpunkt drehe. Der Durchbruch und Erfolg der Keplerschen Berechnungen lag weniger darin begründet, dass die Sonne und nicht mehr die Erde im Mittelpunkt der Bewegungen stand, sondern in der Tatsache, dass Kepler Ellipsenbahnen und keine Kreisbahnen mehr verwendete, was zu einer größeren Übereinstimmung mit den von Tycho Brahe und später Galileo Galilei tatsächlich gemessenen Planetendaten führte.
Kritik
In neuerer Zeit wurden die Leistungen des Ptolemäus jedoch sehr viel kritischer bewertet. Schon Tycho Brahe sprach um 1600 von „Betrug“. 1817 warf ihm der französische Astronom und Mathematiker Jean-Baptiste Joseph Delambre gefälschte und fingierte Beobachtungen, vorgefasste Meinungen, Lügen und Plagiat vor. Dies wurde 1977 und nochmals 1985 durch den englischen Astronomen Robert Russell Newton in vollem Umfang wiederholt. So sollen laut Newton fast alle von Ptolemäus angeblich selbst gemachten Beobachtungen fiktiv oder von Hipparchos übernommen sein, dessen Längenangaben nur 2° 40', der Wert der aufgelaufenen Präzession, hinzugefügt wurden (korrekt wären 3° 40’ gewesen). Diesem vernichtenden Urteil über Ptolemäus hat sich B. L. van der Waerden in seinem 1988 erschienenen Buch „Die Astronomie der Griechen“ angeschlossen.
Andererseits präsentierte bereits 1796 Pierre Simon Laplace eine simple Erklärung: die Differenz von einem Bogengrad lasse sich durch einen gleich großen Fehler in der damaligen Theorie der Sonnenbewegung begründen. Bradley E. Schaefer kam 2002 zu dem Schluss, eine beträchtliche Anzahl der von Ptolemäus genannten Beobachtungsdaten habe dieser (bzw. seine Assistenten) selbst gewonnen. Er habe jedoch dann, wenn fremde, ältere Daten besser zu seinem Modell passten als seine eigenen, diese ohne ausdrückliche Quellenangabe übernommen. Diese Vorgehensweise war zu einer Zeit, in der man an wissenschaftliche Arbeiten noch nicht die heute üblichen Maßstäbe anlegte, durchaus üblich.
Weiteres
Ein weiteres astronomisches Werk des Ptolemäus sind seine „Planetenhypothesen“, in dem er die Ergebnisse des Almagest dazu benutzte, Aussagen über die Dimensionen des Universums im Großen zu treffen. So schätzte er aufgrund seines Modells die mittlere Distanz zur Sonne als 1.210 (tatsächlich: 23.480) und die Distanz zur Fixsternsphäre als 20.000 Erdradien. Gezeigt wird darin auch, wie ein anschauliches mechanisches Modell des Kosmos gebaut werden kann.
Eine weitere vor allem für praktische Zwecke gedachte Sammlung sind seine „Handlichen Tabellen“. In der „Phaseis“ (Aufgänge und Niedergänge der Sterne mit Wetterzeichen) stellte er zudem einen Sternenkatalog basierend auf dem Lauf der Sterne übers ganze Jahr zusammen. Zur Anwendung der Mathematik auf astronomische Fragestellungen stammen von ihm die beiden Schriften „Analemma“ und „Planisphaerium“. Astronomisch auch erwähnenswert ist die auf einer Stele erhaltene „Kanobusinschrift“.
Seinen chronologischen Angaben bezüglich astronomischer Aufzeichnungen ordnet Ptolemäus Daten des ägyptischen Kalenders zu. Um Mehrdeutigkeiten zu vermeiden, nennt er für nächtliche Ereignisse den ausgehenden und beginnenden altägyptischen Tag. Aufgrund jener präzisen Angaben sind die jeweiligen Vorkommnisse im julianischen Kalender exakt datierbar.
Mathematik
Einzig bekanntes eigenständiges mathematisches Werk ist die nur noch bei Proklos überlieferte „Abhandlung über das Parallelenpostulat“, in dem er einen Beweis für das Parallelenaxiom von Euklid geben wollte, der aber mathematisch nachweisbar falsch ist. Andere mathematische Ausführungen wurden in die genannten primär anwendungsorientierten astronomischen Schriften eingearbeitet.
So stammt von ihm der Satz von Ptolemäus. Dieser mathematische Lehrsatz gilt für Sehnenvierecke. (Ein Sehnenviereck ist ein Viereck, zu dem ein Kreis durch alle vier Ecken konstruiert werden kann). Der Satz von Ptolemäus besagt, dass bei einem Sehnenviereck die Summe aus dem Produkt gegenüberliegender Seitenlängen das Produkt der beiden Diagonalen ergibt. Somit gilt ac + bd = ef. Da auch symmetrische Trapeze einen Umkreis haben, erhält man für die symmetrischen Schenkel b = d und den Diagonalen e = f den Sonderfall ac + b2 = e2 . Der Satz gilt ferner auch für Rechtecke, die ebenfalls einen Umkreis haben. Hier gilt dann a = c , so dass der Satz von Ptolemäus den Satz des Pythagoras als Spezialfall enthält: a2 + b2 = e2 . Wie auch der Satz des Pythagoras ist der Satz von Ptolemäus umkehrbar.
Im Almagest (XIII 10) findet sich folgende Konstruktion des regelmäßigen Fünf- bzw. Zehnecks: Zum gegebenen Umkreis (Durchmesser [AB]) des gesuchten Fünf- oder Zehnecks wird der Radius [OB] halbiert (Mittelpunkt M) und der Kreis um M durch C gezeichnet. Der Schnittpunkt dieses Kreises mit dem Durchmesser [AB] ist der Punkt D. Die Strecke [OD] ist die Seite des zugehörigen Zehnecks, die Strecke [CD] ist die Seite des zugehörigen Fünfecks. Der Radius [OC] ist gleichzeitig die Seite des zugehörigen Sechsecks. Die Konstruktion beruht auf zwei Sätzen der Elemente des Euklid (IV 11) und (III 39).
Wichtig zur Vereinfachung seiner astronomischen Berechnungen wurde auch die von Ptolemäus im Almagest (I 10) berechnete Sehnentafel für den Bereich bis mit Schrittweite Solche Sehnentafeln dient als Ersatz für eine Sinus-Tabelle, da gilt:
Als Beispiel für die erreichte Genauigkeit soll die Angabe aus dem Almagest dienen:
Im Sechzigersystem bedeutet dies
Damit wird etwa eine 5-stellige Genauigkeit erreicht, wie der Taschenrechner zeigt:
In der Abbildung gilt:
- und
Im Einheitskreis hat der Satz des Pythagoras dann die Form:
Geographie
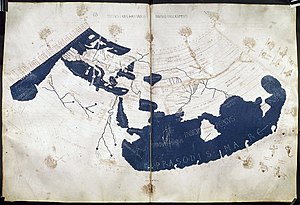
Neben dem zusammenfassenden Kanon bedeutender Städte verfasste Ptolemäus die Geographia (Geographike Hyphegesis, Explicatio geographica, „geografische Anleitung“), in der er die bekannte Welt und ihre Bewohner aufzeichnete.
Als Referenz für die Längengrade (±180°) definierte er den bis in das 19. Jahrhundert verwendeten Meridian durch die von ihm so genannten „makaron nesoi“ (lateinisch: „insulae fortunatae“), die heutigen Kanarischen Inseln (Ferro-Meridian). Seine Definition der Breitengrade ist bis heute gültig (Äquator 0°, Pole ±90°). Außerdem legt er darin seine Hypothese vom unbekannten Südkontinent Terra Australis dar. Ptolemäus war wie früher schon Aristoteles bekannt, dass die Erde eine Kugel ist; er stellte zu deren Darstellung in einer Blattebene mehrere geeignete Projektionen vor. Er nahm auch verschiedene Verbesserungen am früheren Werk des Marinos von Tyros vor. Allerdings nutzte er Informationen aus zweiter Hand oder Legenden, so dass seine Darstellungen, insbesondere der behandelten Völker, oft ungenau oder sogar irreführend sind. Er befasste sich auch mit den Berechnungen des Erdumfangs von Eratosthenes und Poseidonios. Dabei übernahm er die falschen Ergebnisse des Letzteren, die dann in die allgemein bekannte Literatur übergingen und bis zu Christoph Kolumbus auf einen zu geringen Erdumfang von ca. 17.000 Seemeilen (30.000 km) schließen ließen.
Musiktheorie
Ptolemäus schrieb auch die aus drei Büchern bestehende „Harmonik“, das wichtigste erhaltene musiktheoretische Werk der Spätantike nach Aristoxenos und Euklid. Er versuchte – wie wahrscheinlich schon Eratosthenes – einen Kompromiss zwischen Aristoxenos und den Pythagoreern, an dem sich später auch Boethius orientierte. Rechnerisch vertrat er die Position von Euklid, ideell und terminologisch aber die auf der musikalischen Wahrnehmung aufgebaute Lehre des Aristoxenos. Er überlieferte in seiner Harmonik viele Details älterer antiker Musiktheoretiker, etwa die Tetrachorde (Tongeschlechter) von Archytas, Eratosthenes und Didymos, die ansonsten verloren wären.
Optik und Erkenntnistheorie
Sein Werk Optik befasst sich mit den Eigenschaften des Lichtes. Er behandelt experimentell und mathematisch unter anderem die Reflexion, Brechung und Farben. Daneben werden optische Täuschungen erwähnt. In der philosophischen Abhandlung peri kriteriou kai hegemonikou (lat. de iudicandi facultate et animi principatu, „Von der Urteilskraft und dem Verstand“) vertritt er eine Mischung aus neuplatonischen und stoischen Anschauungen.
Daneben verfasste er auch das zweiteilige Werk Kriterion zur Erkenntnistheorie, nach dem für das Erkennen von Wahrheit allein die Vernunft genügt. Dabei geht er auch auf das Denken von Tieren ein und bestimmt das sogenannte Hegemonikon, das Funktionszentrum des Körpers, einerseits zum „Leben“ im Herzen und anderseits zum Fällen ethischer Entscheide d.h. zum „Gut Leben“ im Gehirn.
Astrologie
Ptolemäus schrieb weiterhin in 4 Bänden das bis heute nachwirkende astrologische Grundlagenwerk Tetrabiblos („vier Bücher“; griechisch Ἀποτελεσματικά Apotelesmatika). Dieses Werk basiert auf seinen astronomischen Schriften und beschreibt die Auswirkungen der Himmelskörper auf die Menschen und deren Schicksal.
Siehe auch
Textausgaben
- Johan Ludvig Heiberg (Hrsg.): Claudii Ptolemaei opera quae exstant omnia. Teubner, Leipzig, Band I (Syntaxis, also Almagest) in zwei Bänden 1898, 1903, Band II (Opera astronomica minora), 1907. Der Teil III, 1 (Tetrabiblos) wurde von Franz Boll, Emilie Boer herausgegeben und erschien 1954 (und 1998 bearbeitet von Wolfgang Hübner), Teil III, 2 (Fragmente, zweifelhafte Werke) wurde 1952, 1961 von Friedrich Lammert herausgegeben.
- Claudius Ptolemäus: Tetrabiblos. Nach der von Melanchthon besorgten seltenen Ausgabe aus dem Jahre 1553. 2. Auflage. Chiron, Tübingen 2000, ISBN 3-925100-17-2.
- Frank E. Robbins (Hrsg.): Ptolemy Tetrabiblos, Loeb Classical Library, Harvard University Press 1940
- Ingemar Düring: Die Harmonielehre des Klaudios Ptolemaios. Elander, Göteborg, 1930; Nachdruck Olms, Hildesheim 1982.
- Jon Solomon (Hrsg.): Ptolemy. Harmonics, Mnemosyne, Bibliotheca Classica Batava, Supplementum, Leiden: Brill 2000 (englische Übersetzung)
- A. M. Smith (Hrsg.): Ptolemy's theory of visual perception: An English translation of the Optics with introduction and commentary, Transactions of the American Philosophical Society, Band 86, Teil 2, Philadelphia 1996
- A. Lejeune (Hrsg.): L´optique de Claude Ptolémée, Löwen 1956 und Leiden: Brill 1989 (Latein/Französisch)
Für die Ausgaben des Almagest und Geographike Hyphegesis und Literatur dazu siehe dort.
Literatur
- Jacqueline Feke, George Saliba: Ptolémée d'Alexandrie (Claude). In: Richard Goulet (Hrsg.): Dictionnaire des philosophes antiques, Band 5, Teil 2 (= V b), CNRS Éditions, Paris 2012, ISBN 978-2-271-07399-0, S. 1718–1735
- Gerald J. Toomer in Dictionary of Scientific Biography
- Bartel Leendert van der Waerden in Pauly-Wissowa, und zur Geographie E. Polaschek in Supplement X, 1965
- Otto Neugebauer A history of ancient mathematical astronomy, 3 Bände, Springer Verlag 1975
- Franz Boll Studien über Claudius Ptolemaeus. Ein Beitrag zur Geschichte der griechischen Philosophie und Astrologie. In: Neue Jahrbücher für Philologie und Pädagogik. Supplementband 21,2. Teubner, Leipzig 1894, S. 49–244
- Alexander Jones (Hrsg.): Ptolemy in perspective: use and criticism of his work from antiquity to the nineteenth century, Springer 2010
- Klaus Geus: Ptolemaios – Reaktionär, Theoretiker, Plagiator?. In: Thomas Beck, Marília dos Santos Lopes, Christian Rödel (Hrsg.): Barrieren und Zugänge. Die Geschichte der europäischen Expansion. Festschrift für Eberhard Schmitt zum 65. Geburtstag. Harrassowitz, Wiesbaden 2004, ISBN 3-447-04848-4, S. 36–50.
- Gerd Graßhoff: The history of Ptolemy’s star catalogue. Springer, New York NY u. a. 1990, ISBN 0-387-97181-5.
- Wilfried Neumaier: Was ist ein Tonsystem? Eine historisch-systematische Theorie der abendländischen Tonsysteme, gegründet auf die antiken Theoretiker, Aristoxenos, Eukleides und Ptolemaios, dargestellt mit Mitteln der modernen Algebra. Lang, Frankfurt am Main u. a. 1986, ISBN 3-8204-9492-8.
- Ingemar Düring: Ptolemaios und Porphyrios über die Musik. Göteborg 1934, Nachdruck Olms, Hildesheim 1987, ISBN=3-487-07932-1
Weblinks
Commons: Claudius Ptolemäus – Sammlung von Bildern
- Literatur von und über Claudius Ptolemäus im Katalog der Deutschen Nationalbibliothek
- Claudius Ptolemäus. In: MacTutor History of Mathematics archive (englisch)
- Zum Satz des Ptolemäus, Landesbildungsserver Baden-Württemberg
- Klaudios Ptolemaios als Geograph
- Literatur zur Geographie (Geographike Hyphegesis) des Claudius Ptolemaeus
- Biographie de Ptolémée (französisch)
- Werke von Claudius Ptolemäus im Gesamtkatalog der Wiegendrucke
Texte
Almagest
- Almagest Bücher 1-6 – griechischer Text mit lateinischer Einleitung im Internet Archive
- Almagest Bücher 1-13 – griechischer Text (Ausgabe von Heiberg, PDF)
- Almagest – Digitalisat einer Ausgabe von 1515 (Universität Wien, lateinische Übersetzung, mehrere Auflösungen, PDF)
Geographike
- Claudii Ptolemaei Geographia, ed. 1843, tom. I (Bücher 1–4); 1845, tom. II (Bücher 5–8); 1845, tom. III (Register) – griechischer Text der Tauchnitz-Ausgabe (Google Books)
- Geographike – analytischer Auszug mehrerer Kapitel, Germania Magna und andere griechisch/lateinisch/englisch, weitere nur englisch
- Geographie – LacusCurtius (englische Übersetzung, Bücher 2-5, nicht alle Abschnitte vorhanden, klickbare Karten entsprechend Ptolemäus’ Koordinatenangaben)
- Claudii Ptholemaei Alexandrini liber geographiae cum tabulis et universali figura et cum additione locorum quae a recentioribus reperta sunt diligenti cura emendatus et impressus – lateinische Übersetzung (Venedig 1511, Digitalisat der University of Alabama)
- Geographike Buch 8 – griechischer Text von Aubrey Diller (PDF)
Tetrabiblos
- Tetrabiblos auf LacusCurtius (englische Übersetzung, unvollständig)
- Tetrabiblos vollständige englishe Übersetzung von J.M. Ashmand (1822)
- Claudius Ptolemaeus: Ptolemaei libri IV mathematicae translatione Wintomiensis Ebdelmessiae - Mscr.Dresd.Db.87. [S.l.] 1450, Digitalisat der Sächsischen Landesbibliothek
Digitalisate
- Cosmographia Claudii Ptolomaei Alexandrini (1467) – Digitalisat der Biblioteka Narodowa
- Johannes Regiomontanus, Georg von Peuerbach, Claudius Ptolemaeus: Ioannis De Monte Regio Et Georgii Purbachii Epitome, In Cl. Ptolemaei Magnam compositionem. Basileae 1543, Digitalisat der Sächsischen Landesbibliothek
Fußnoten
- ↑ G. J. Toomer: Ptolemy. In: Dictionary of Scientific Biography. Band 11, New York 1976, S. 186-206.
| Personendaten | |
|---|---|
| NAME | Ptolemäus, Claudius |
| ALTERNATIVNAMEN | Πτολεμαῖος, Κλαύδιος (griechisch); Ptolemaíos, Klaúdios; Ptolomaeus, Claudius (lateinisch) |
| KURZBESCHREIBUNG | griechischer Mathematiker, Geograph und Astronom |
| GEBURTSDATUM | um 100 |
| GEBURTSORT | Ptolemais Hermeiou, Ägypten |
| STERBEDATUM | vor 180 |
| STERBEORT | Alexandria, Ägypten |
| Dieser Artikel basiert ursprünglich auf dem Artikel Claudius Ptolemäus aus der freien Enzyklopädie Wikipedia und steht unter der Doppellizenz GNU-Lizenz für freie Dokumentation und Creative Commons CC-BY-SA 3.0 Unported. In der Wikipedia ist eine Liste der ursprünglichen Wikipedia-Autoren verfügbar. |