Mittelsenkrechte

Mittelsenkrechte

Mittellotebene

(S): In der ebenen Geometrie ist die Mittelsenkrechte oder das Mittellot oder (österreichisch) die Streckensymmetrale diejenige Gerade durch den Mittelpunkt einer Strecke, die auf der Strecke senkrecht steht.

Die Verallgemeinerung auf drei Dimensionen ist die Mittellotebene einer Strecke.

Anwendungen:
Mittelsenkrechten tragen oft zur Lösung von geometrischen Problemen bei, z. B.
a) bei der zeichnerischen Bestimmung des Mittelpunktes einer Strecke, um einen Thaleskreis zu konstruieren,
b) bei der Bestimmung des Umkreismittelpunktes eines Dreiecks,
c) bei der zeichnerischen Rekonstruktion des Mittelpunktes eines Kreises, wenn 3 Punkte des Kreises gegeben sind,
d) bei der Bestimmung einer Geraden oder Ebene, um durch Spiegeln an dieser einen Punkt $A$ auf einen Punkt $B$ abzubilden.
e) In Voronoi-Diagrammen spielen sie eine Rolle als Begrenzungen.

Weitere Definitionen

In der Ebene

Zur Definition (S) in der Einleitung sind die folgenden Definitionen (D) und (M2) äquivalent:

(D): Die Mittelsenkrechte einer Strecke $AB$ ist die Menge aller Punkte $X$ mit der Eigenschaft $|XA|=|XB|$.

Der Beweis (siehe Bild im nächsten Abschnitt) folgt aus der Eigenschaft $|MA|=|MB|$ des Mittelpunktes $M$ und dem Satz des Pythagoras:

$|XA|^{2}=|XM|^{2}+|MA|^{2}=|XM|^{2}+|MB|^{2}=|XB|^{2}\;.$

Die Gleichung $|XA|=|XB|$ lässt sich auch so interpretieren: $X$ ist der Mittelpunkt eines Kreises, der durch $A$ und $B$ geht. Damit gibt es die weitere Definition:

(M2): Die Mittelsenkrechte einer Strecke $AB$ ist die Menge der Mittelpunkte aller Kreise, die durch $A,B$ gehen.

Im Raum

Geht man von Punkten $A,B$ im 3-dimensionalen Raum aus, so definiert man (analog zum ebenen Fall):

(D): Die Mittellotebene einer Strecke $AB$ ist die Menge aller Punkte $X$ mit der Eigenschaft $|XA|=|XB|$.

Der Nachweis der Äquivalenz zur Definition in der Einleitung verläuft analog zum ebenen Fall.

Konstruktion der Mittelsenkrechten und des Mittelpunktes

Konstruktion der Mittelsenkrechten

Aufgrund der Definition (D) der Mittelsenkrechten und der Tatsache, dass eine Gerade durch zwei Punkte eindeutig bestimmt ist, genügt es, zwei Punkte $X_{1},X_{2}$ zu finden mit der Eigenschaft $|X_{i}A|=|X_{i}B|$:

Mittelsenkrechte

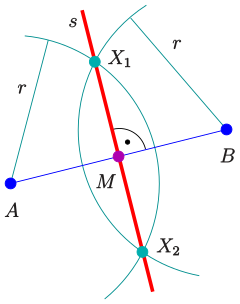
Man konstruiert die Mittelsenkrechte zu zwei gegebenen Punkten $A$ und $B$, indem man um diese beiden Punkte mit einem Zirkel Kreisbögen zeichnet mit gleichem Radius, der größer als die halbe Länge der Strecke zwischen den beiden Punkten sein muss. Die zwei Schnittpunkte $X_{1},X_{2}$ dieser beiden Kreislinien bestimmen die Mittelsenkrechte der Strecke $AB$.

Mittelpunkt

Da die Konstruktion der Mittelsenkrechten ohne Kenntnis des Mittelpunktes $M$ auskommt, kann man den Mittelpunkt als Schnitt der so konstruierten Mittelsenkrechten mit der Strecke $AB$ bestimmen.

Gleichungen

Sind ${\vec {a}},{\vec {b}}$ und ${\vec {m}}:={\tfrac {{\vec {a}}+{\vec {b}}}{2}}$ die Ortsvektoren der Punkte $A,B$ und $M$, so ist $M$ der Mittelpunkt von $A,B$ und ${\vec {a}}-{\vec {b}}$ ein Normalenvektor der Mittelsenkrechten. Eine Normalenform der Mittelsenkrechten ist dann $({\vec {x}}-{\vec {m}})\cdot ({\vec {a}}-{\vec {b}})=0$. Ersetzen von ${\vec {m}}$ durch ${\tfrac {{\vec {a}}+{\vec {b}}}{2}}$ und Ausmultiplizieren liefert die Gleichung der Mittelsenkrechten in Vektorform:

(V): $\quad {\vec {x}}\cdot ({\vec {a}}-{\vec {b}})={\tfrac {1}{2}}({\vec {a}}^{2}-{\vec {b}}^{2}).$

Mit $A=(a_{1}|a_{2})$ und $B=(b_{1}|b_{2})$ erhält man die Koordinatenform:

(K2): $\quad (a_{1}-b_{1})x+(a_{2}-b_{2})y={\frac {1}{2}}(a_{1}^{2}-b_{1}^{2}+a_{2}^{2}-b_{2}^{2}).$

Falls $b_{2}\neq a_{2}$, kann man zur expliziten Form (siehe Orthogonalität und Punktsteigungsform)

(E2):$\quad y=m(x-x_{0})+y_{0}$

mit $\;m=-{\tfrac {b_{1}-a_{1}}{b_{2}-a_{2}}}$, $\;x_{0}={\tfrac {1}{2}}(a_{1}+b_{1})\;$ und $\;y_{0}={\tfrac {1}{2}}(a_{2}+b_{2})\;$ übergehen.

Die Vektordarstellung der Mittellotebene ist wörtlich gleich mit (V). Die Koordinatendarstellung ist um eine Koordinate erweitert:

(K3): $\quad (a_{1}-b_{1})x+(a_{2}-b_{2})y+(a_{3}-b_{3})z={\frac {1}{2}}(a_{1}^{2}-b_{1}^{2}+a_{2}^{2}-b_{2}^{2}+a_{3}^{2}-b_{3}^{2})\ .$

Beispiele

Für jede Position der Strecke ${\overline {AB}}$ (grün) auf der zu ihr rechtwinkligen Geraden $g_{1}$ (blau) gilt für die Mittelsenkrechte $m_{s}$ (rot) die Geradengleichung $4x+8y=5$

In der Ebene

${\overline {AB}}$ (grün) sei die Strecke mit den Endpunkten $A=(2{,}5|-5)$ und $B=(6|2)$. Dann ist $a_{1}=2{,}5,\;b_{1}=6,\;a_{2}=-5$ und $b_{2}=2.$

Setzt man diese Werte in die obige Koordinatengleichung (K2) ein, so ergibt sich für die Geradengleichung der Mittelsenkrechten:

${\begin{aligned}(2{,}5-6)x+(-5-2)y&={\frac {2{,}5^{2}-6^{2}}{2}}+{\frac {(-5)^{2}-2^{2}}{2}}\\-3{,}5x-7y&=-{\frac {8{,}75}{2}}\,{\bigg |}\,\cdot (-2)\\7x+14y&={\frac {17{,}5}{2}}\,{\bigg |}\,\cdot {\frac {4}{7}}\\4x+8y&=5\end{aligned}}$

Im Raum

Für $A=(2|1{,}5|1)$ und $B=(1|2{,}5|5)$ ergibt sich aus der obigen Gleichung (K3) die Koordinatengleichung der Mittellotebene

${\begin{aligned}x-y-4z&=-12{,}5\,\Leftrightarrow \\2x-2y-8z&=-25.\end{aligned}}$

Die Mittellotebene (blau) verläuft rechtwinklig zur Strecke ${\overline {AB}}$ (grün) durch deren Mittelpunkt $M$ (rot)

Mittelsenkrechten im Dreieck

Die Mittelsenkrechten eines Dreiecks schneiden sich in einem Punkt, nämlich im Umkreismittelpunkt des Dreiecks. Dieser Umkreis geht durch alle Ecken des Dreiecks (siehe dazu auch: Ausgezeichnete Punkte im Dreieck).

Im gleichschenkligen Dreieck kann die Mittelsenkrechte, für den Winkel am Scheitel der beiden gleichen Schenkel, auch die Funktion der Winkelhalbierenden erfüllen. Dies ist insbesondere dann vorteilhaft, wenn der Scheitel nicht innerhalb der Zeichenebene liegt.

Mittelsenkrechte im gleichschenkligen Dreieck quasi als Winkelhalbierende; der Scheitel liegt außerhalb der Zeichenebene

Dreieck mit Mittelsenkrechten und Umkreis

Siehe auch

• Symmetrale

Literatur

• Rolf Baumann: Geometrie. Mit Übungen und Lösungen. Mentor, München 2002, Kapitel 3.1.
• Cornelia Niederdrenk-Felgner: Lambacher-Schweizer. Lehrbuch der Mathematik für die 7. Klasse (G9) an Gymnasien (Baden-Württemberg). Klett, Stuttgart 1994, ISBN 3-12-731370-5.

Weblinks

Wiktionary: Mittelsenkrechte – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen