SIR-Modell

Zeitlicher Verlauf der drei Gruppen S, I und R mit den Startwerten ${\textstyle S_{0}=997,I_{0}=3,R_{0}=0}$ sowie Infektionsrate ${\textstyle \beta =0,0004}$ und Rate ${\textstyle \gamma =0,04}$ für die Gruppe R. In dieser Variante des Modells sind die Parameter wie folgt zu substituieren, wenn sie mit den unten genannten Differentialgleichungen übereinstimmen sollen: ${\textstyle \beta ={\frac {c}{N}},\gamma =w}$.

Stehen weder Medikamente noch eine Impfung zur Verfügung, so kann man nur die Zahl der Ansteckungen durch geeignete Maßnahmen reduzieren. Diese Animation zeigt, wie sich eine Senkung der Infektionsrate um 76 % (von ${\textstyle \beta =0,0005}$ auf ${\textstyle \beta =0,00012}$) auswirkt (die übrigen Parameter sind wie in der Grafik oben ${\textstyle S_{0}=997,I_{0}=3,R_{0}=0}$ sowie ${\textstyle \gamma =0,004}$).

Als SIR-Modell (Susceptible-Infected-Removed-Model) bezeichnet man in der mathematischen Epidemiologie, einem Teilgebiet der Theoretischen Biologie, einen klassischen Ansatz zur Beschreibung der Ausbreitung von ansteckenden Krankheiten mit Immunitätsbildung, der eine Erweiterung des SI-Modells darstellt.

Voraussetzungen

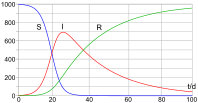
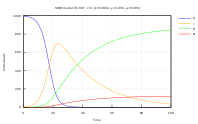
Beim SIR-Modell werden drei Gruppen von Individuen unterschieden: Zum Zeitpunkt $t$ bezeichnet $S(t)$ die Anzahl der gegen die Krankheit nicht immunen Gesunden (susceptible individuals), $I(t)$ die Zahl der reversibel und ansteckenden Infizierten (infectious individuals) sowie $R(t)$ die Anzahl der aus dem Krankheitsgeschehen „entfernten“ Personen (removed individuals; nach erworbener Immunität gegen die Krankheit bzw. durch Tod). Weiterhin sei $N$ die Gesamtzahl der Individuen. Das SIR-Modell kann für Krankheiten verwendet werden, die folgende Eigenschaften aufweisen:

• Jedes Individuum kann von einem Erreger nur einmal infiziert werden und wird danach entweder immun oder stirbt.
• Die Zahl der Individuen ist konstant, d. h. es gilt der Zusammenhang $S(t)+I(t)+R(t)=N\ \forall t\geq 0$. Todesfälle werden zur Gruppe R gezählt, Geburten nicht berücksichtigt.
• Infizierte sind sofort ansteckend.
• Gesunde werden mit der linearen Rate $c\geq 0$ infiziert.
• Infizierte gehen mit der linearen Rate $\omega \geq 0$ in die Gruppe R über, womit sie aus dem Infektionsgeschehen ausscheiden.
• Jede Gruppe interagiert miteinander mit derselben Wahrscheinlichkeit. Dies rechtfertigt die Annahme linearer Zusammenhänge.
• Alle Parameter bleiben im biologisch sinnvollen Bereich, also $S(t),I(t),R(t)\in [0,\infty )$.

Das Verhältnis ${\frac {S}{N}}$ repräsentiert dabei die Wahrscheinlichkeit, dass ein Kontakt suszeptibel (ansteckbar) ist; die Gesundungsrate $c$ ist das Produkt aus der mittleren Anzahl der Kontakte pro Person und der Infektionsrate pro Kontakt.

Differentialgleichungen des SIR-Modells

Da wir einen linearen Zusammenhang zwischen allen Messgrößen als Voraussetzung annehmen, lassen sich die folgenden gewöhnlichen Differentialgleichungen formulieren:

$${\begin{aligned}{\frac {dS}{dt}}&=-c{\frac {S}{N}}I&&(1)\\{\frac {dI}{dt}}&=c{\frac {S}{N}}I-\omega I&&(2)\\{\frac {dR}{dt}}&=\omega I&&(3)\end{aligned}}$$

wobei die Nebenbedingung

$$N=S+I+R$$

zu erfüllen ist.

• Gleichung (1) beschreibt, wie sich die Anzahl der nicht-immun Gesunden S bei Begegnung mit einem Infizierten reduziert.
• Gleichung (3) beschreibt, wie sich nach Ende der Krankheit die Zahl der Immunen, zu der die Toten gezählt werden, erhöht.
• Gleichung (2) beschreibt schließlich, wie sich die Zahl der Kranken, ansteckenden Personen durch die in (1) bzw. (3) beschriebenen Effekte erhöht bzw. erniedrigt.

Um dimensionslose Größen zu erhalten sei vereinbart:

$u_{1}:={\frac {S}{N}},u_{2}:={\frac {I}{N}},u_{3}:={\frac {R}{N}},\theta :=\omega t,r:={\frac {c}{\omega }}$

Damit schreiben sich obige Gleichungen als:

$${\begin{aligned}{\frac {du_{1}}{d\theta }}&=-ru_{1}u_{2}\\{\frac {du_{2}}{d\theta }}&=ru_{1}u_{2}-u_{2}\\{\frac {du_{3}}{d\theta }}&=u_{2}\end{aligned}}$$

Die Nebenbedingung transformiert sich zu $1=u_{1}+u_{2}+u_{3}$. Es sollen folgende Anfangsbedingungen gelten:

$${\begin{aligned}S(0)=S_{0}\geq 0&&I(0)=I_{0}\geq 0&&R(0)=0.\end{aligned}}$$

Offensichtlich ist dann die Nebenbedingung erfüllt: ${\dot {S}}(t)+{\dot {N}}(t)+{\dot {R}}(t)=0\Rightarrow N=S+I+R=I_{0}+S_{0}$. Daher sollte dieses Modell nur für kurzfristige Epidemien verwendet werden, in denen Geburten und Tode vernachlässigbar klein sind.

Da die Differentialgleichung für $u_{3}$ bzw. für $R$ linear von den ersten beiden Differentialgleichungen abhängt, kann im weiteren die Projektion des Zustandsraumes auf die $u_{1}u_{2}$-Ebene betrachtet werden: Für $r>1$ schneidet, wie man an der Steigung abliest, die Isokline (von $u_{2}$) $ru_{1}-1=0$ das Dreieck ${u_{1},u_{2}|u_{1}+u_{2}<=1}$ und die Krankheitsverbreitung hat einen Fixpunkt. Für $r<1$ existiert dieser Fixpunkt nicht und die Krankheit verschwindet.

Eng verwandt ist die Lotka-Volterra-Gleichung. Eine gemeinsame Behandlung erfahren diese Modelle in der Theorie der Replikatordynamiken.

Epidemie

Mit Hilfe des SIR-Modells können wir für gegebene Anfangswerte $I_{0},S_{0},c,\omega$ bestimmen, ob der Krankheitsverlauf in einer Epidemie münden wird. Diese Frage ist äquivalent zu der Frage, ob die Zahl der Infizierten zum Zeitpunkt $0$ steigt. Betrachte die Ableitung:

$\left.{\frac {\mathrm {d} I}{\mathrm {d} t}}\right|_{t=0}=I_{0}(cS_{0}-\omega )>0\ \ {\text{für }}S_{0}>\rho :={\frac {\omega }{c}}$.

Hierbei nennen wir $\rho$ den Schwellenwert einer Epidemie, da aus $S(t)\leq S_{0}$ für alle Zeiten die Ungleichung ${\dot {S}}\leq 0$ für alle $t\geq 0$ folgt und für $S_{0}<\rho$ die obige Behauptung zum Auftreten einer Epidemie gilt:

${\dot {I}}(t)=I(cS-\omega )\leq 0\ \forall t\geq 0$.

Eine Epidemie tritt im SIR-Modell also genau dann auf, wenn $S_{0}>\rho$ ist.

Maximale Zahl der Infizierten

Aus den obigen Differentialgleichungen für $I$ und $S$ folgt:

${\frac {\mathrm {d} I}{\mathrm {d} S}}=-{\frac {(cS-\omega N)I}{cSI}}=-1+{\frac {N\rho }{S}}$.

Integration durch Trennung der Variablen liefert:

$I(t)+S(t)-N\rho \ln S(t)=I_{0}+S_{0}-N\rho \ln S_{0}={\text{const.}}$

Die maximale Zahl der Infizierten ergibt sich offensichtlich für $S_{0}\geq \rho$ und bei $S(t)=\rho$. Mit der obigen Gleichung ergibt sich:

$I_{\text{max}}=-N\rho +N\rho \ln(N\rho )+I_{0}+S_{0}-N\rho \ln S_{0}=N\left(1-\rho +\rho \ln \left({\frac {N\rho }{S_{0}}}\right)\right).$

Zahl der Überlebenden

Es stellt sich auch die Frage, ob die Epidemie überhaupt überlebt wird. Dazu berechnen wir $S(\infty )$. Analog ergibt sich aus den obigen Differentialgleichungen

${\frac {\mathrm {d} S}{\mathrm {d} R}}=-{\frac {S}{\rho }}$, deren Lösung $S=S_{0}\exp \left(-{\frac {R}{\rho }}\right)\geq S_{0}\exp \left(-{\frac {N}{\rho }}\right)>0$ ist.

Damit folgt offensichtlich $0<S(\infty )<N$, es wird also nicht die gesamte Population infiziert. Es zeigt sich, dass es am Ende einer Epidemie weniger an Gesunden als eher an Infizierten mangelt!

Näherungen: Reduziere Zahl der Parameter

Wenn wir die Anfangswerte $I_{0},S_{0},c,\omega$ kennen, können wir mit den obigen Differentialgleichungen schnell die Dynamik einer Krankheit bestimmen. Oft lassen sich aber gerade diese Konstanten nur schwer bestimmen, weshalb wir im Folgenden die obigen Gleichungen nähern wollen.

Aus den besprochenen Differentialgleichungen folgt sofort

$${\begin{aligned}{\frac {\mathrm {d} R}{\mathrm {d} t}}=\omega (N-R-S)=\omega \left(N-R-S_{0}\exp \left(-{\frac {R}{\rho }}\right)\right).\end{aligned}}$$

Die Gleichung vereinfacht sich zu einer Riccatischen Differentialgleichung, wenn $\exp \left(-{\frac {R}{\rho }}\right)$ durch die ersten 3 Summanden der Taylorreihe um ${\frac {R}{\rho }}=0$ angenähert wird:

$${\begin{aligned}{\frac {\mathrm {d} R}{\mathrm {d} t}}&=\omega \left(N-S_{0}\right)+\omega \left({\frac {S_{0}}{\rho }}-1\right)R-\omega {\frac {S_{0}}{2\rho ^{2}}}R^{2}\\&=-\omega {\frac {S_{0}}{2\rho ^{2}}}R^{2}+\omega \left({\frac {S_{0}}{\rho }}-1\right)R+\omega \left(N-S_{0}\right),\end{aligned}}$$

also

$${\begin{aligned}R(t)&={\frac {\rho ^{2}}{S_{0}}}\left(\left({\frac {S_{0}}{\rho }}-1\right)+\alpha \operatorname {tanh} \left({\frac {\alpha \omega t}{2}}-\phi \right)\right)\\\alpha &={\sqrt {\left({\frac {S_{0}}{\rho }}-1\right)^{2}+2{\frac {S_{0}(N_{0}-S_{0})}{\rho ^{2}}}}}\\\phi &={\frac {\tanh ^{-1}\left({\frac {S_{0}}{\rho }}-1\right)}{\alpha }}.\end{aligned}}$$

Damit lässt sich die Differentialgleichung für $R$ mit nur drei Parametern aufschreiben:

$${\frac {\mathrm {d} R}{\mathrm {d} t}}={\frac {\omega \alpha ^{2}\rho ^{2}}{2S_{0}}}\operatorname {sech} ^{2}\left({\frac {\alpha \omega t}{2}}-\phi \right),$$

nämlich $\alpha \omega$, $\phi$ und ${\frac {\omega \alpha ^{2}\rho ^{2}}{2S_{0}}}$. Je nach Datenlage kann hierbei die Differentialgleichung oder die implizite Gleichung für $R(t)$ verwendet werden.

Erweiterung des Modells

Zeitlicher Verlauf der vier Gruppen S, I, R und D mit den Startwerten S=997, I=3, R=0 sowie Infektionsrate $\beta =0,0004$ (identisch mit Werten der Grafik für das SIR-Modell oben), einer Rate $\gamma =0,035$ für die Gruppe R sowie Sterberate $\mu =0,005$

Will man die Toten separat betrachten (statt zur Gruppe R hinzuzurechnen), so kann man es zum SIRD-Modell (Susceptible-Infected-Recovered-Deceased-Model) erweitern. Hierbei gehören zur Gruppe R nur die Individuen, welche die Krankheit überlebt haben und immun geworden sind, und die Gestorbenen bilden eine eigene Gruppe D.

Siehe auch

• Mathematische Modellierung der Epidemiologie (einführender Artikel)
• SI-Modell (Ansteckung ohne Gesundung)
• SIS-Modell (Ausbreitung von ansteckenden Krankheiten ohne Immunitätsbildung)
• Dynamisches System (mathematischer Oberbegriff)

Literatur

• N. F. Britton: Essential Mathematical Biology. 1. Auflage. Springer, Berlin 2003, ISBN 1-85233-536-X.