Spirale

Die Spirale als Emblem der 20. Olympischen Sommerspiele

Eine Spirale oder Schneckenlinie ist eine Kurve, die um einen Punkt oder eine Achse verläuft und sich je nach Laufrichtung von diesem/r entfernt oder annähert.

Spirale oder Schraube

Die Spirale wird manchmal mit der Schraube verwechselt. Während die prototypische Spirale ein Gebilde in der Ebene ist, wie zum Beispiel die Rille einer Schallplatte, oder die Arme einer Spiralgalaxie, ist sowohl die Schraube als auch der Wendelbohrer ein räumliches Gebilde entlang des Hofes eines Zylinders.

Spiraltypen

Ebene Spiralen

Die Zentralprojektion einer Schraube (grün) auf eine ebene Fläche erzeugt eine hyperbolische Spirale (schwarz)

Man kann diese Spiralen mathematisch am besten als Koordinatengleichungen im ebenen Polarkoordinatensystem beschreiben, wobei r als Funktion von Φ dargestellt wird; Φ läuft im Allgemeinen bis unendlich anstatt nur bis 2π. Im Folgenden sind jeweils eine Formel für r(Φ) und die Länge s der Spirale ab Φ = 0 angegeben.

Die archimedische Spirale entsteht z. B. beim Aufwickeln eines gleichmäßig dicken Teppichs.

$r(\phi )=a\cdot \phi$

$s(\phi )={\frac {a}{2}}\cdot \left(\ln \left({\sqrt {\phi ^{2}+1}}+\phi \right)+\phi \cdot {\sqrt {\phi ^{2}+1}}\right)$

Die beim Aufwickeln benötigte Materiallänge (speziell beim Schmieden dekorativer Spiralen) lässt sich mit Hilfe von Clacksons Spiralenformel (die den Winkel in Anzahl von Umrundungen also in Vollwinkel angibt) abschätzen zu $\approx {\frac {a}{2}}\phi ^{2}$ durch die Taylorreihennäherung 1. Ordnung der Bogenlänge.

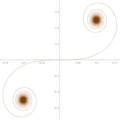
Die logarithmische Spirale entsteht z. B. beim Wachstum von Schneckenhäusern.

$r(\phi )=b\cdot e^{a\cdot \phi }$

Länge vom Koordinatenursprung ($\phi =-\infty$) weg:

$s(\phi )={\frac {b\cdot e^{a\cdot \phi }\cdot {\sqrt {a^{2}+1}}}{a}}$

Die hyperbolische Spirale sieht man z. B. beim senkrechten Blick durch eine Wendeltreppe.

$r(\phi )={\frac {a}{\phi }}$

In dieser Gleichung läuft die Spirale mit wachsendem Φ von außen (unendlich ferner Punkt bei Φ=0) nach innen; die Entfernung auf der Spirale von einem beliebigen Punkt der Spirale bis zum Koordinatenursprung ist jedoch auch unendlich, deshalb ist hier die Entfernung zwischen zwei Punkten mit den Winkeln Φ und Θ angegeben.

$s(\phi ,\theta )=a\cdot \left({\frac {\sqrt {\phi ^{2}+1}}{\phi }}-{\frac {\sqrt {\theta ^{2}+1}}{\theta }}-\ln \left(\left({\sqrt {\phi ^{2}+1}}+\phi \right)\cdot \left({\sqrt {\theta ^{2}+1}}-\theta \right)\right)\right)$

Es existieren noch viele weitere bekannte mathematische Funktionen, die ebene Spiralen erzeugen.

• 

  Archimedische Spirale $r=a\phi$

• 

  Logarithmische Spirale $\ln r-\ln b=a\phi$

• 

  Fermatsche Spirale $r^{2}=a\phi$

• 

  Hyperbolische Spirale $r\phi =a$

• 

  Lituus-Spirale $r^{2}\phi =a$

• 

  Spirale des Theodorus (Wurzelschnecke) $r\to a\phi$

• 

  Klothoide (Cornu-Spirale)

Dreidimensionale Spiralen

Konische Spirale (rot), Schraube (grün) und archimedische Spirale (schwarz)

Ouroboros, gerendert

Konische Spirale entlang eines Kreises

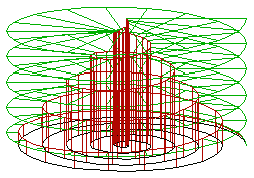
In einem Kreiszylinder kann man eine archimedische Spirale auf den Boden legen und eine Schraube als Kurve in den Mantel einpassen. Die Überlagerungskurve von Spirale und Schraube wird als konische Spirale oder kegelförmige Raumspirale bezeichnet.

Krümmt man den Zylinder nun zu einem Torus, entsteht eine andere Raumspirale (frei nach M. C. Escher, siehe in den unten stehenden Links).

Der dieser Zeichnung zugrunde liegende Kegelmantel erinnert an das Ouroboros-Motiv, und kann als ein Torus mit stetig zunehmenden Ringdurchmesser aufgefasst werden.

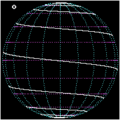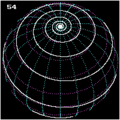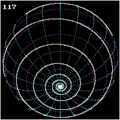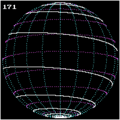
Bei einer archimedischen Spirale vergrößert sich der Abstand zum Mittelpunkt linear zum anwachsenden Winkel ihres Umlaufes. Wird dieser Abstand als Winkelabstand zu einem Pol auf eine Kugeloberfläche projiziert, entsteht eine archimedische Kugelspirale. Sie ist eine Linie von endlicher Länge, und nicht mit der Loxodrome identisch, welche durch ihr Konstruktionsverfahren der logarithmische Spirale ähnelt.

• 

  Archimedische Kugelspirale

• 

  Loxodrome

Spiralmotive auf Bildsteinen

Triplespirale als vorzeitliches Motiv (Triskele)

In der Kirche von Vallstena wurde ein gotländischer Bildstein gefunden, dessen Mittelteil mit einem vierfachen Spiralornament verziert ist. Das Zeichen, das als Triplespirale wesentlich älter ist und z.B. im Passage tomb von Newgrange in Irland vorkommt, ist auf Gotland als 4-, 6- und 7-fache Kombination anzutreffen. Auch stilisierte Tierköpfe sowie realistischere Bilder von Menschen und Tieren sind bisweilen mit dem geometrischen Motiv vereint. Es handelt sich bei der Spirale, ebenso wie beim Wirbelrad, vermutlich um ein Sonnensymbol oder die Darstellung einer Göttervielheit. Farbe unterstützte das flache, aber fein gehauene Ornament und hob die Darstellung hervor. Das Spiralmotiv kommt in verschiedener Form und Komposition auf den älteren Steinen, die zwischen 400 – 600 n. Chr. entstanden vor. Spiralmotive tauchen aber sowohl früher als auch später in verschiedenen Fundzusammenhängen auf. Auf den Britischen Inseln sind sie um Christi Geburt verbreitet und in der mehrere Jahrhunderte jüngeren spätkeltischen Kunst können sie in frühchristlichen Handschriften studiert werden. Diese Kunst steht den Bildsteinen zeitlich näher; es ist daher vermutet worden, dass ein gewisser Zusammenhang besteht.

Sozialwissenschaften

In der Demoskopie wurde die Metapher „Schweigespirale“ von Elisabeth Noelle-Neumann benutzt, um ein bestimmtes gegenseitiges sich Aufschaukeln von sozialen Reaktionen zu erklären und zugleich zu bekämpfen: In der öffentlichen Meinung würden gewisse Minderheitenstandpunkte so nachdrücklich vertreten, dass die Mehrheit zögere, sich überhaupt zu äußern, darauf würde die Minderheit immer diktatorischer und die Mehrheit immer stummer usw. Empirisch ist dieser Zusammenhang sehr schwer zu überprüfen.

Allgemein wird bei jedem Mechanismus, der eine Eskalation des Zustandes bewirkt, von einer Spirale gesprochen, etwa „Spirale der Gewalt“. In der Systemwissenschaft zeigen harmonische Oszillatoren, die exponentiell anwachsen (eskalieren), logarithmische Spiralen in ihren Phasendiagrammen (Eskalationsspirale). Daher ist dieser Begriff mathematisch korrekter als der synonym gebrauchte Begriff „Teufelskreis“, der keine Eskalation der Zustände beinhaltet.

Spiralen in der Natur

Gehäuse einer Schnecke

Sonnenblume mit 34 und 55 Fibonacci-Spiralen

Viele Pflanzen und manche Tiere weisen in ihrem Bauplan spiralige Strukturen auf wie zum Beispiel das Schneckenhaus.. Die "Anordnung" dieser biologisch erzeugten Spiralen, welche meistens auf logarithmischen Spiralen beruhen, wiederum erfolgt in den allermeisten Fällen als Fibonacci-Folge.

Siehe auch

• Ulam-Spirale
• Intrauterinpessar, umgangssprachlich auch „Spirale“ genannt, eine Methode der Empfängnisverhütung

Weblinks

 Commons: Spiralen und Schrauben – Sammlung von Bildern, Videos und Audiodateien

• Mathematische Basteleien: Spiralen
• Beispiele für Spiralen im Pflanzenreich