| Jewiki unterstützen. Jewiki, die größte Online-Enzyklopädie zum Judentum.
Helfen Sie Jewiki mit einer kleinen oder auch größeren Spende. Einmalig oder regelmäßig, damit die Zukunft von Jewiki gesichert bleibt ... Vielen Dank für Ihr Engagement! (→ Spendenkonten) |
How to read Jewiki in your desired language · Comment lire Jewiki dans votre langue préférée · Cómo leer Jewiki en su idioma preferido · בשפה הרצויה Jewiki כיצד לקרוא · Как читать Jewiki на предпочитаемом вами языке · كيف تقرأ Jewiki باللغة التي تريدها · Como ler o Jewiki na sua língua preferida |
Halbton
Halbton (lateinisch semitonium, auch griech./lat. hemitonium) bezeichnet in der Musik das kleinste Intervall des heute verbreiteten zwölfstufigen Tonsystems. In Ausnahmefällen wird die Bezeichnung auch auf einzelne Töne angewendet (siehe unten).
Halbton als Intervall
Die Intervallbezeichnung Halbton ersetzt in griffiger Kurzform die vollständigeren Bezeichnungen Halbtonschritt oder Halbtonabstand.
Die Musiktheorie unterscheidet zwischen dem diatonischen Halbton (kleine Sekunde, z. B. g→as) und dem chromatischen Halbton (übermäßige Prime, z. B. as→a), die zusammen einen Ganzton ergeben. Selten findet der enharmonische Halbton (doppelt verminderte Terz, z. B. fis→asas) Erwähnung.
Je nach Stimmung und musikalischem Zusammenhang sind die einzelnen Halbtöne schwach hörbar verschieden.
Gleichstufig temperierter Halbton
Im gleichstufig temperierten Tonsystem entspricht der Halbton einem Zwölftel der Oktave. Diese Bedeutung wurde bereits von Aristoxenos vorweggenommen, indem er die Oktave in sechs gleiche Ganztöne teilte und den Halbton als die Hälfte eines Ganztons definierte.
Die rechnerisch exakte Zwölftelung der Oktave ergibt für den temperierten Halbton ein Frequenzverhältnis (Proportion) von Cent, da dieser Wert zwölfmal mit sich selbst multipliziert das Frequenzverhältnis einer Oktave (2/1) ergibt.
Halbtöne der pythagoreischen Stimmung
In pythagoreischen Tonsystemen tritt aufgrund der reinen Quinten (Proportion 3⁄2) kein (aus dem unteren Bereich der Obertonreihe stammender) „natürlicher“ Halbton ( 16⁄15) auf, sondern das Intervall mit der Proportion Cent,[1] das bei Philolaos „Diesis“, bei Euklid „Leimma“, seit der Spätantike auch als Halbton bezeichnet wurde.
Ohne praktische Verwendung wurde auch als Halbton die Apotome ( Cent) bezeichnet: die Differenz zwischen Ganzton ( 9⁄8) und Leimma ( 256⁄243). Die Tonbuchstaben und die Notenschrift unterscheiden diese Intervalle klar: Das Leimma ist eine kleine Sekunde c-h, die Apotome ein chromatischer Schritt, nämlich die übermäßige Prime cis→c.
Den Unterschied hebt erst die gleichstufige Stimmung auf, da sie das pythagoreische Komma (= Apotome-Leimma) zum Verschwinden bringt und dadurch eine enharmonische Verwechslung ermöglicht.
Kleiner und großer Halbton der harmonisch-reinen Stimmung
Die Einbeziehung der reinen großen Terz mit der Proportion 5⁄4 in der seit der Renaissance aufkommenden reinen Stimmung änderte die Größenordnung der Halbtöne. Der diatonische Halbton, der große Halbton mit der Proportion kann nun dem unteren Bereich der Obertonreihe zugeordnet werden.
Wegen der Existenz von zwei Ganztönen gibt es auch zwei chromatische Halbtöne (übermäßige Primen), die kleinen Halbtöne mit den Proportionen und .
Beispiel:
| Name des Tones | C | CIS | D | DIS | E | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Frequenz | 264 | 278,4 | 297 | 309,3 | 330 | ||||||
| In Cent (gerundet) | 0 | 92 | 204 | 275 | 386 | ||||||
| Halbton in Cent | 92 | 112 | 71 | 112 | |||||||
| Name des Tones | C | DES | D | ES | E | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Frequenz | 264 | 281,6 | 297 | 316,8 | 330 | ||||||
| In Cent (gerundet) | 0 | 112 | 204 | 316 | 386 | ||||||
| Halbton in Cent | 112 | 92 | 112 | 71 | |||||||
Noch heute gilt bei Intonationen von a-cappella-Chören die folgende Faustregel (Regel des Weißenburger Kantors Maternus Beringer, 1610).[2]
„Halbtöne auf derselben Linie im Notensystem (die chromatischen) sind als kleiner Halbton (semitonus minor) zu intonieren. Halbtöne auf benachbarten Linien (die diatonischen) aber als großer Halbton (semitonus major).“
Wie man der Frequenztabelle und der Grifftabelle von Peter Prelleur entnehmen kann, sind die mit einem Kreuz bezeichneten Töne CIS, DIS usw. tiefer als die mit einem b bezeichneten DES, ES usw.
Diese harmonische Intonation steht im Gegensatz zur expressiven Intonation, bei der die Leittöne (Cis Leitton zu D, Dis zu E, Des zu C, Es zu D und so weiter) enger gespielt werden.
Musikbeispiele
Musikbeispiel 1: Akkorde hier nach „Selig seid ihr“ EKG Württemberg Nr. 651
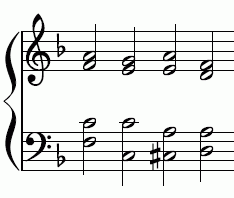
|
|
| Tonschritt im Bass | in reiner Stimmung | in mitteltöniger Stimmung | in gleichstufiger Stimmung |
|---|---|---|---|
| C-Cis | 71 Cent | 76 Cent | 100 Cent |
| Cis-D | 112 Cent | 112 Cent | 100 Cent |
Musikbeispiel 2: Passus duriusculus. Akkorde hier nach W.A. Mozart „Misericordias Domini“ d-Moll (KV 205 a).

|
Die Halbtonschritte im Bass betragen in der reinen Stimmung |
c → h: 112 Cent |
Tabellarische Übersicht
Als ein Hundertstel des gleichstufigen Halbtons wurde gegen Ende des 19. Jahrhunderts die Intervalleinheit Cent festgelegt. Sie erlaubt einen besonders klaren Größenvergleich bei den verschiedenen Halbtönen:
Die Halbtöne der pythagoreischen Tonleiter
- bzw. …
| Intervall | Frequenzverhältnis | in Cent | Beispiel |
|---|---|---|---|
| Ganzton | 9⁄8 | 204 Cent | C-D |
| Halbton Leimma | 256⁄243 | 90 Cent | E-F |
| Halbton Apotome | 2187⁄2048 | 114 Cent | B-H |
Die Apotome ist ein rein rechnerisches Intervall. In der mittelalterlichen Musik werden nie die beiden Töne B und H gleichzeitig verwendet.
Die Halbtöne der reinen Tonleiter
| Intervall | Frequenzverhältnis | in Cent | Beispiel |
|---|---|---|---|
| großer Ganzton | 9⁄8 | 204 Cent | C-D |
| kleiner Ganzton | 10⁄9 | 182 Cent | D-E |
| diatonischer Halbton | 16⁄15 | 112 Cent | E-F |
| großer chromatischer Halbton | 135⁄128 | 92 Cent | C-Cis |
| kleiner chromatischer Halbton | 25⁄24 | 71 Cent | B-H |
Die Halbtöne der 1/4-Komma mitteltönigen Tonleiter
Die Frequenzverhältnisse sind – bis auf die Oktave ( 2⁄1) und große Terz ( 5⁄4) – irrational. Deshalb wird die Intervallgröße in Cent angegeben.
- C – 193 Cent – D – 193 Cent – E – 117 Cent – F – 193 Cent – G – 193 Cent – A – 193 Cent – H – 117 Cent – C
| Intervall | Größe in Cent | Beispiel |
|---|---|---|
| Ganzton | 193 Cent | C-D |
| diatonischer Halbton | 117 Cent | E-F |
| chromatischer Halbton | 76 Cent | C-Cis |
Die Halbtöne der gleichstufigen Tonleiter
- C – 200 Cent – D – 200 Cent – E – 100 Cent – F – 200 Cent – G – 200 Cent – A – 200 Cent – H – 100 Cent – C
| Intervall | Größe in Cent | Beispiel |
|---|---|---|
| Ganzton | 200 Cent | C-D |
| diatonischer Halbton | 100 Cent | E-F |
| chromatischer Halbton | 100 Cent | C-Cis |
Zusammenfassung
| Intervall | Proportion | Größe in Cent |
|---|---|---|
| Zwölfter Teil der Oktave | 100 Cent | |
| Leimma | 256⁄243 | ≈90 Cent |
| Apotome | 2187⁄2048 | ≈114 Cent |
| diatonischer Halbton | 16⁄15 | ≈112 Cent |
| großer chromatischer Halbton | 135⁄128 | ≈92 Cent |
| kleiner chromatischer Halbton | 25⁄24 | ≈71 Cent |
| diatonischer mitteltöniger Halbton | ≈117 Cent | |
| chromatischer mitteltöniger Halbton | ≈76 Cent | |
| Vincenzo-Galilei-Halbton-Näherung | 18⁄17 | ≈99 Cent |
Chromatische Tonleiter
Eine zwölfstufige Tonleiter ausschließlich aus Halbtonschritten wird chromatische Tonleiter genannt. Darin lösen sich der diatonische Halbtonschritt = kleine Sekunde und der
chromatische Halbtonschritt = übermäßige Prime folgerichtig ab. Im folgenden Beispiel der von c1 ausgehenden chromatischen Skala sind die chromatischen Halbtonschritte daran zu erkennen, dass Ausgangs- und Zielton auf gleich hohen Positionen im Liniensystem notiert sind, während bei diatonischen Halbtonschritten die entsprechenden Notenpositionen unterschiedlich sind.

Hörbeispiele
- Halbton aufwärts
- Halbton abwärts
Halbton als Einzelton
Gelegentlich wird der Ausdruck Halbton auch auf einzelne Töne bezogen.
- In der Tonwort-Methode von Carl Eitz wird die Bezeichnung Halbton für eine einzelne Stufe der chromatischen Tonleiter verwendet, während die Stammtöne als Ganztöne bezeichnet werden. Die Ganztöne bilden im Rahmen dieser Ausdrucksweise eine Teilmenge der gesamten Halbtonmenge.
- In der Vergangenheit wurden auch gelegentlich (in heute unüblicher Weise) die Stammtöne (weiße Tasten der Klaviatur) als Ganztöne und deren chromatische Varianten (schwarze Tasten der Klaviatur) als Halbtöne bezeichnet. Johann Sebastian Bach zielt offensichtlich auf diese Bedeutung ab, wenn er auf dem Titelblatt seines Wohltemperierten Klaviers von „Præludia und Fugen durch alle Tone und Semitonia“ spricht. Klavierbauer pflegen diesen Sprachgebrauch noch heute (2018).[3]
Siehe auch
- Kleiner und großer Halbton bei der reinen Stimmung und mitteltönigen Stimmung
- Intervalltabellen
Weblinks
Einzelnachweise
- ↑ Dieser Halbtonschritt ergibt sich als Quarte − 2 Ganztöne. Das Frequenzverhältnis errechnet sich demnach zu 4⁄3 × 8⁄9 × 8⁄9 = 256⁄243 (siehe pythagoreische Stimmung).
- ↑ Diese Regel wurde in vielen alten Gesangsschulen formuliert. Hier nach Maternus Beringer: Musicae, das ist der freyen lieblichen Singkunst. Georg Leopold Fuhrmann, Nürnberg 1610 (Nachdruck: Bärenreiter, Kassel 1974).
- ↑ https://www.pianoteile-baumgaertel.de/?pgid=12QQ3YOLC6OGRSY3SGN12F9TM&ecskey=t9tg7fqhusq07f3fdhigiphbj1
| Dieser Artikel basiert ursprünglich auf dem Artikel Halbton aus der freien Enzyklopädie Wikipedia und steht unter der Doppellizenz GNU-Lizenz für freie Dokumentation und Creative Commons CC-BY-SA 3.0 Unported. In der Wikipedia ist eine Liste der ursprünglichen Wikipedia-Autoren verfügbar. |
![{\displaystyle {\sqrt[{12}]{2}}{\widehat {=}}{\text{100}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e682c258b60b402b6ddef8dc14efa41143b69d0b)





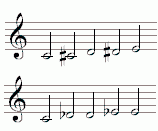




![{\displaystyle {\sqrt[{12}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc835f27425fb3140e1f75a5faa35b1e8b9efc35)
![{\displaystyle {\frac {8}{25}}{\sqrt[{4}]{5^{3}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32b025ec5bcc566bc9c034b690f16ce5aea82149)
![{\displaystyle {\frac {5}{16}}{\sqrt[{4}]{5^{3}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9bd43ef9d885a5b5b4a6aa946f92ab933659b1e)